中2数学の最後に「箱ひげ図」があります。
これは最近中学校に追加されたもので、そのためか受験にも頻出しています。わかりづらいので解説ページを作りました。
100人の箱ひげ図で、「25人を4分割」 のとき
①中央値を求めましょう
全員で100人なら、50人と50人に分けられます。
ぴったり2分割できるので、中央の人がいないため、50人目と51人目の平均が中央値です。
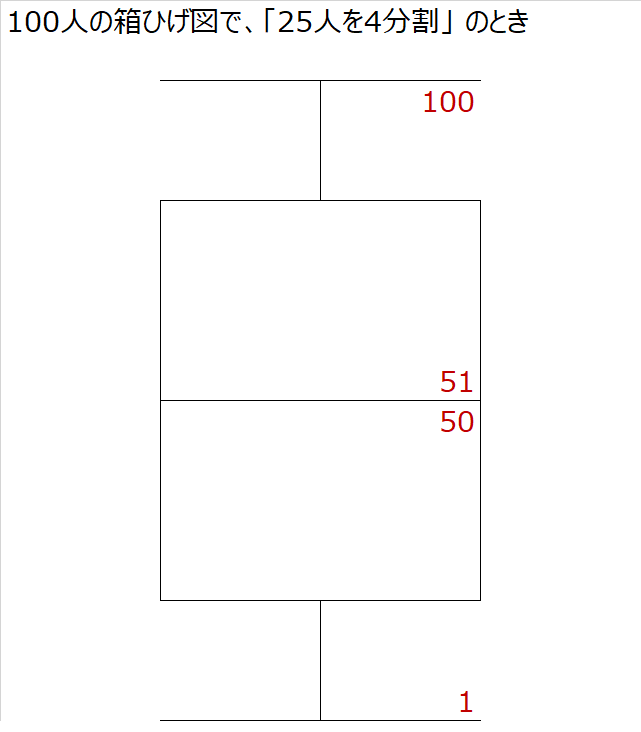
②前半の半分、後半の半分を求めよう
50人を、25人ずつの2つに分けます。
前半は、1~25、26~50
後半は、51~75、76~100
に分けられます。
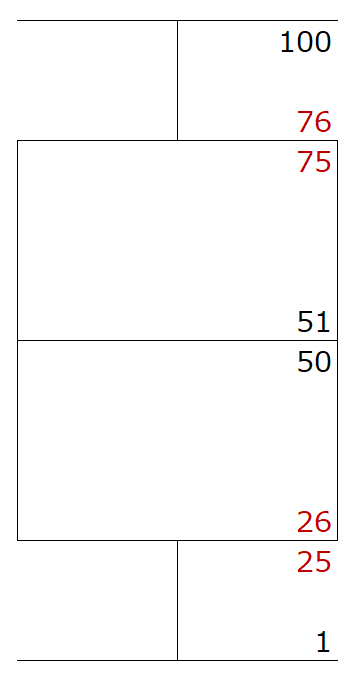
50人を25人ずつに分けると、ちょうどど真ん中がいないので、25人と26人の平均が前半の中央値(第一四分位数)になります。7
75人と76人の平均が後半の中央値(第三四分位数)になります
箱ひげ図でわかりづらければ、下図のように25人を4分割で考えるのも手です。
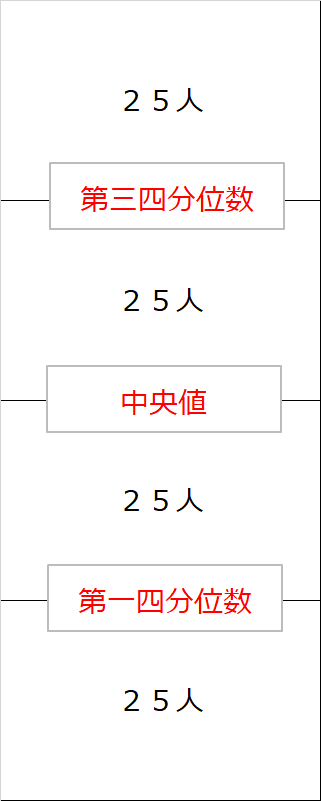
やや応用編「棒の中の、どこに多くいるかは、わからない」
最小値から25人目までの棒。均等に人数がいると思ってはいけません。下の方に固まっている可能性があります。

「〇点以下の生徒は、〇人いるか?」のような人数を数えるときに「わからない」となりやすいのが棒だけの部分です。
-120x68.png)
